一、总结

1. 这篇论文要解决什么问题？

作者总结了两个脑网络分析中带来噪声的问题。子人群分布变化：分析神经疾病应该捕捉在所有人群中不变的疾病特性，然而，某些特征对于子种群（不能推广到整个种群），并且与疾病无关，会构成特定子人群的噪声。忽视节点身份：一般GNN不考虑节点身份，针对脑网络的已有工作也考虑节点身份了，但是它们不考虑子人群分布变化。

2. 已有工作的思路以及不足之处有哪些？

已有工作主要是基于GNN和Graph Transformer。不足之处即没考虑上述两个问题，同时，先前研究还发现一个GNN的问题是过度平滑。在本文背景下，基于相关性的脑网络图天然具有高密度（全连接图），很容易受到过度平滑的影响。

3. 作者的洞见（insight）有哪些？

看起来本文是对作者先前的工作ContrastPool（Contrast Graph）和CARE（Cluster Loss）的改进和应用。

4. 解决方法的基本思想是什么？

同时考虑不同（标签的）组的图级信息、节点身份。

二、方法

问题定义为脑网络矩阵的分类任务。模型主要包括三个部分：（1）对比图编码器，引入对比图编码器解决子人群分布变化问题，不同组之间的脑网络通过ROI-wise注意力和subject-wise注意力（即双流注意力）聚合生成对比图，对比图将为测试提供先验知识。（2）交叉解码器，将输入的大脑网络与节点身份结合，随后通过交叉注意力将其与对比图结合。（3）分类损失和三个辅助损失共同实现端到端优化。辅助损失强调了ROI的节点身份，并考虑了组级关系。

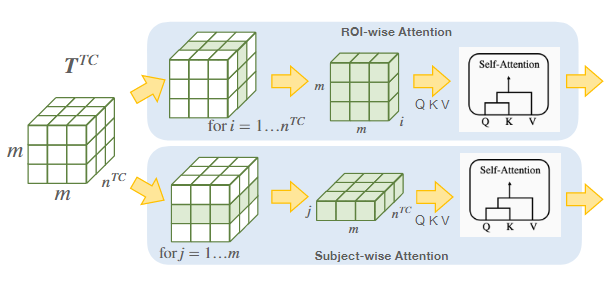
双流注意力+对比图编码器：双流注意力是从ROI和受试者两个维度分别执行的自注意力，以TC组会例，计算TC组的总结图：

Hsum TC=1nTC∑i=1nTC(HROITC+Hsubject TC)(i,:,:),HROITC=[Attn⁡ROI(TTC(i,:,:)):i=1,…,nTC],HsubjectTC=[Attn⁡subject(TTC(:,j,:)):j=1,…,m],\begin{gathered} H_{\text {sum }}^{T C}=\frac{1}{n^{T C}} \sum_{i=1}^{n^{T C}}\left(H_{R O I}^{T C}+H_{\text {subject }}^{T C}\right)(i,:,:), \\ H_{R O I}^{T C}=\left[\operatorname{Attn}_{R O I}\left(T^{T C}(i,:,:)\right): i=1, \ldots, n^{T C}\right], \\ H_{subject }^{T C}=\left[\operatorname{Attn}_{subject }\left(T^{T C}(:, j,:)\right): j=1, \ldots, m\right], \end{gathered}

这里的HROITCH_{R O I}^{T C}和HsubjectTCH_{subject }^{T C}表示注意力输出分数。通过计算所有总结图的方差来生成对比图，对比图会包含组间差异（group-discriminative information），而去除了组无关信息（均值）。对比图只在训练阶段学习，测试阶段会被作为先验信息输入。

身份嵌入+交叉解码器：基于距离的、基于中心性和基于特征向量的位置嵌入。由于其高密度(总是完全连接的)，很难迁移到大脑网络。基于相关性的大脑网络天然包含足够的 ROI 位置信息，所以通用的图位置嵌入是多余的。本文提出了一种可学习的身份嵌入，自适应学习每个ROI的身份信息:

HID(l)=H(l−1)+δ(H(l−1)+WID(l−1))H_{I D}^{(l)}=H^{(l-1)}+\delta\left(H^{(l-1)}+W_{I D}^{(l-1)}\right)

这个里的输出作为QQ，对比图作为KK和VV计算交叉注意力，用对比图作为先验知识知道脑网络表示学习。

损失函数全家桶：总损失函数包括四项，

Ltotal =Lcls +λ1∗Lentropy +λ2∗Lcluster +λ3∗Lcontrast ,\mathcal{L}_{\text {total }}=\mathcal{L}_{\text {cls }}+\lambda_1 * \mathcal{L}_{\text {entropy }}+\lambda_2 * \mathcal{L}_{\text {cluster }}+\lambda_3 * \mathcal{L}_{\text {contrast }},

防止平滑的对比度图对所有ROI一视同仁，引入稀疏约束。采用熵损失，迫使模型优先考虑最特定于任务的ROI连接。

Lentropy =1m∑i=1mentropy⁡(Hcontrast (i,:)), entropy (p)=−∑j=1mpjlog⁡(pj)\begin{gathered} \mathcal{L}_{\text {entropy }}=\frac{1}{m} \sum_{i=1}^m \operatorname{entropy}\left(H_{\text {contrast }}(i,:)\right), \\ \text { entropy }(p)=-\sum_{j=1}^m p_j \log \left(p_j\right) \end{gathered}

簇损失强制属于同一组的受试者获得相似的表示，而来自不同组的表示相异。

Lcluster =log⁡exp⁡(∑c∈Cσc2)exp⁡(∑c∈C∑i∈C∥μc−μi∥2)μc=∑k∈Schgk∣Sc∣,σc2=∑k∈Sc(hgk−μc)2∣Sc∣,\begin{gathered} \mathcal{L}_{\text {cluster }}=\log \frac{\exp \left(\sum_{c \in C} \sigma_c^2\right)}{\exp \left(\sum_{c \in C} \sum_{i \in \mathcal{C}}\left\|\mu_c-\mu_i\right\|_2\right)} \\ \mu_c=\sum_{k \in \mathcal{S}^c} \frac{\boldsymbol{h} g^k}{\left|\mathcal{S}^c\right|}, \quad \sigma_c^2=\sum_{k \in \mathcal{S}^c} \frac{\left(\boldsymbol{h g ^ { k }}-\mu_c\right)^2}{\left|\mathcal{S}^c\right|}, \end{gathered}

对比损失将属于同一ROI的节点视为正对，所有其他节点对都被视为负对。

Lcontrast =−log⁡∑(Hji,Hjp)∈Pposexp⁡(sim⁡(Hji,Hjp)/τ)∑(Hji,Hrq)∈Pnegexp⁡(sim⁡(Hji,Hrq)/τ).\mathcal{L}_{\text {contrast }}=-\log \frac{\sum_{\left(H_j^i, H_j^p\right) \in \mathcal{P} p o s} \exp \left(\operatorname{sim}\left(H_j^i, H_j^p\right) / \tau\right)}{\sum_{\left(H_j^i, H_r^q\right) \in \mathcal{P} n e g} \exp \left(\operatorname{sim}\left(H_j^i, H_r^q\right) / \tau\right)} .

三、实验

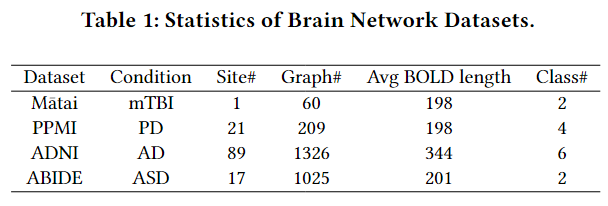
预处理过的ADNI脑网络数据集目前还未公开。第一次接触ADNI数据库，遇到的问题是不理解筛选条件的含义，同一受试者下多个MRI的区别，不知道该下载哪些作为原始数据，目前看到的脑网络相关论文都没有讲这些细节。实验等复现完再写。