黑盒大模型的高效指令优化

InstructZero: Efficient Instruction Optimization for Black-Box Large Language Models

University of Maryland, 5 Jun 2023

数据、代码：https://github.com/Lichang-Chen/InstructZero

简介

对于不能反向传播的闭源大模型，怎么优化指令提示是一个挑战。作者没有直接优化离散的指令，而是优化输入开源大模型的低维soft prompt，以生成闭源大模型的指令。 在每次迭代中，使用开源大模型将软提示转换为指令，然后将其提交给闭源大模型进行zero-shot评估，并将评估性能输入给贝叶斯优化产生新的软提示，提高zero-shot性能。

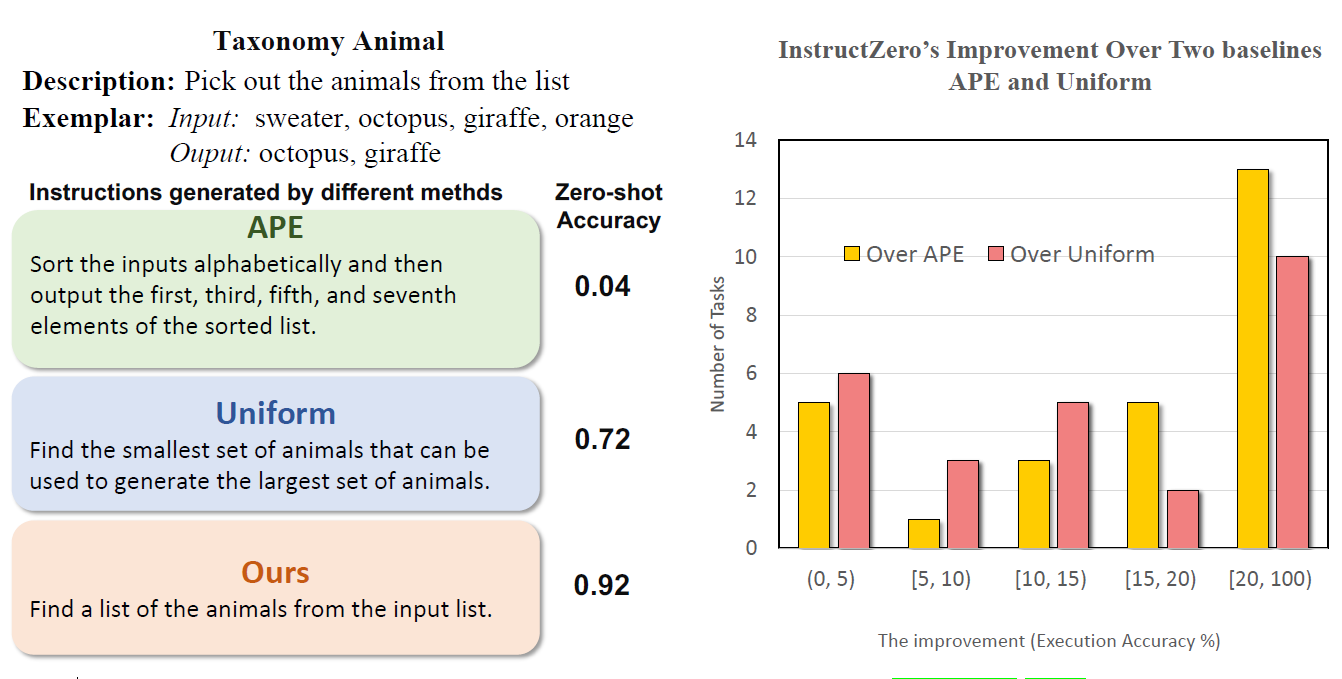比较INSTRUCTZERO和基线方法（ APE [Zhou et al., 2022] 和均匀采样（uniform sampling））

指令优化问题定义

黑盒大模型：$f(\cdot)$

输入的query: $X$

指令：$v\in V$

评价指标：$h(\cdot,\cdot)$

真实标签：$Y$

优化目标，即最大化从任务$t$的数据分布$D_t$中取一个样本$(X,Y)$的期望分数：

$\max _{v \in \mathcal{V}} \mathbb{E}_{(X, Y) \sim \mathcal{D}_t} h(f([v ; X]), Y)$

但是这个公式存在两个挑战：

（1）复杂结构约束的组合优化。指令$v$的优化空间$V$是高维、离散的，在语义约束下高度结构化，目前不存在这种空间进行优化的

高效算法。

（2）黑盒优化，无法直接进行方向传播。

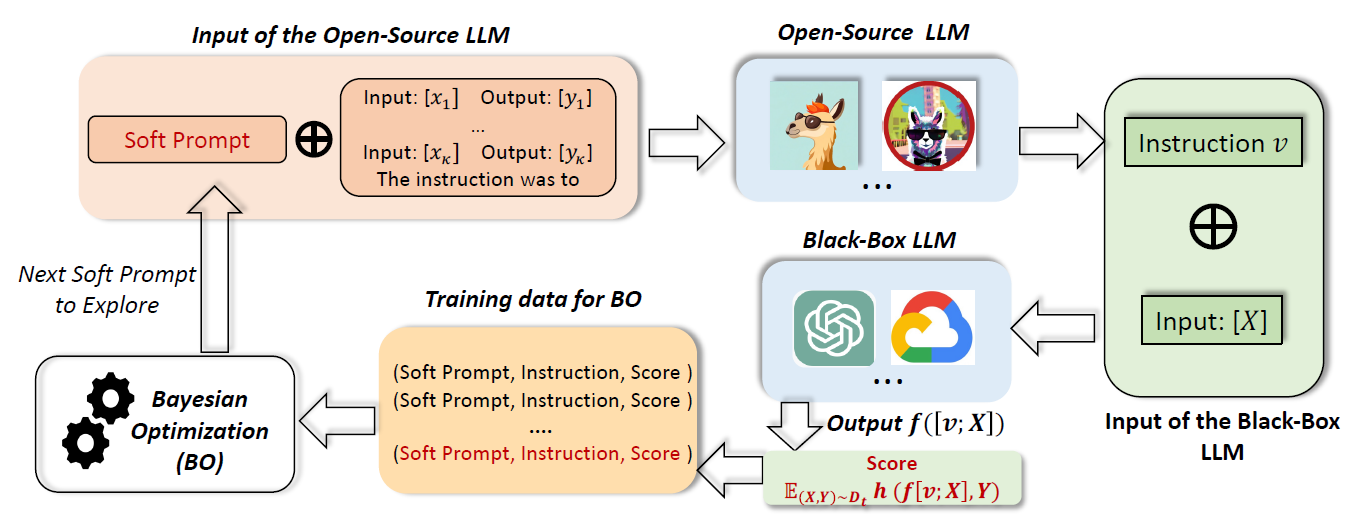
既然无法直接优化$v$，INSTRUCTZERO的核心思想是优化一个soft prompt $p$，$p$输入到开源大模型（LLaMa）$g(\cdot)$，通过针对目标任务的In-context learning（$\kappa$个示例），开源大模型再输出自然语言指令$v$。$v$输入到黑盒大模型产生zero-shot预测结果和性能分数用来评估期望分数，再通过贝叶斯优化（Bayesian optimization）产生新的soft prompt。

具体来说，将一个$d^{\prime}$维的soft prompt $\boldsymbol{p} \in \mathbb{R}^{d^{\prime}}$，以及$\kappa$个示例$\left(x_i, y_i\right)_{i=1}^\kappa$（token embedding）输入到开源大模型$g(\cdot)$，生成的指令$v$再输入到闭源大模型。因此组合优化问题可以被重构为一个可行的连续优化问题：

$\max _{\boldsymbol{p} \in \mathbb{R}^{d^{\prime}}} \mathbb{E}_{(X, Y) \sim \mathcal{D}_t} h(f([v ; X]), Y) \text {, s.t. } v=g\left(\left[\boldsymbol{p} ;\left(x_i, y_i\right)_{i=1}^\kappa\right]\right)$

对于现在开源大模型的来说，维度太高无法直接用现有的黑盒优化方法进行处理，因此需要降维操作。INSTRUCTZERO使用一个矩阵$A\in\mathbb{R}^{d\times d^{\prime}}$（高斯分布或者均匀分布初始化）将soft prompt $\boldsymbol{p}\in \mathbb{R}^{d}$映射到低维隐空间（$d\ll d^{\prime}$）。这样做的目的是：（1）根据Johnson-Lindenstrauss 引理，随机投影保留了距离，（2）通过In-context learning，低维soft prompt足以产生丰富多样且与任务相关的指令作为候选。所以问题变为最大化一个低位空间黑盒函数$H(\boldsymbol{p})$的最大值：

$H(\boldsymbol{p}) \triangleq \mathbb{E}_{(X, Y) \sim \mathcal{D}_t} h(f([v ; X]), Y), \quad v=g\left(\left[A \boldsymbol{p} ;\left(x_i, y_i\right)_{i=1}^\kappa\right]\right)$

基于Instruction-Coupled Kernel的贝叶斯优化

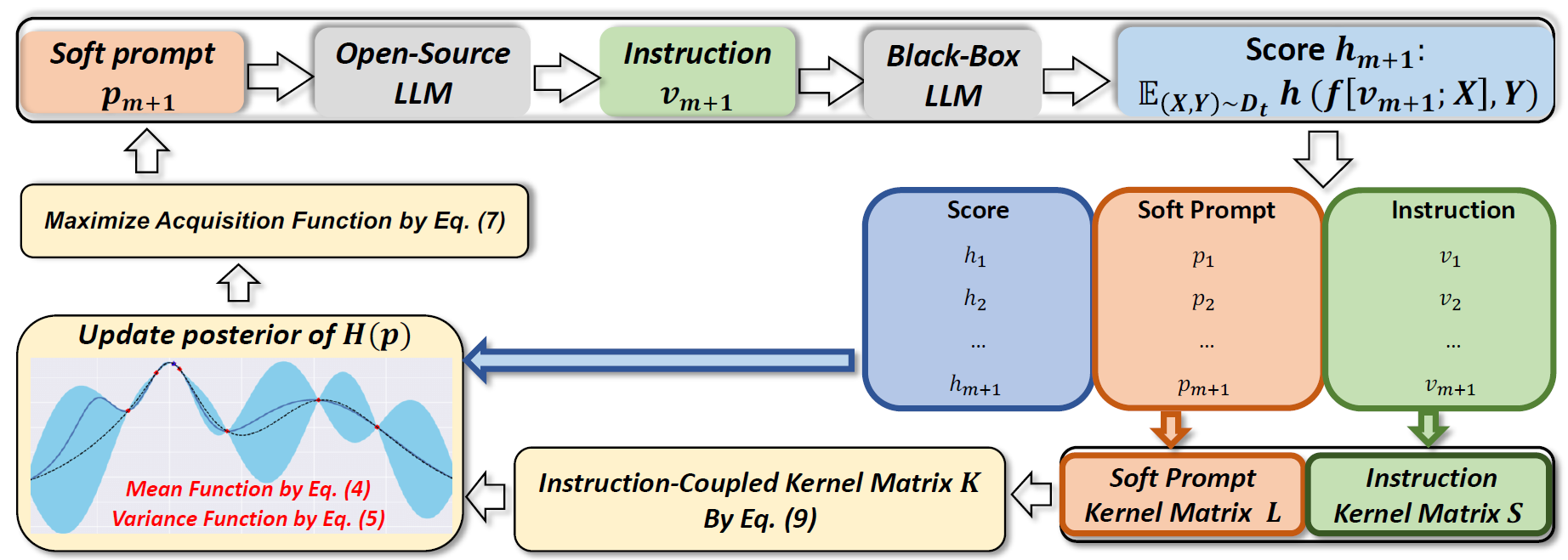
贝叶斯优化的目的是评估黑盒目标函数$H(\boldsymbol{p})$并找到最大值，根据收集的 $(\boldsymbol{p},H(\boldsymbol{p}))$不断更新$H(\boldsymbol{p})$的后验并探索新的soft prompt ，直到$H(\boldsymbol{p})$收敛到最大值（评估性能分数为在验证集的平均结果）。这里使用常用的高斯过程（Gaussian Process）作为黑盒目标函数的先验。高斯过程先验可以由一个均值函数$\mu(\cdot)$和一个协方差函数（即核函数）$\boldsymbol{k}(\cdot,\cdot)$确定。给定$m$个提示和他们的评估结果，$H(\cdot)$的估计后验被作为一个高斯分布进行更新，其中均值函数和方差函数定义如下：

$\begin{gathered} \mu(\boldsymbol{p}) \triangleq \boldsymbol{k}\left(\boldsymbol{K}+\eta^2 \boldsymbol{I}\right)^{-1} H_{1: m} \\ \sigma^2(\boldsymbol{p}) \triangleq k(\boldsymbol{p}, \boldsymbol{p})-\boldsymbol{k}^{\top}\left(\boldsymbol{K}+\eta^2 \boldsymbol{I}\right)^{-1} \boldsymbol{k} \end{gathered}$

$\boldsymbol{K}$表示相应的高斯过程中的核函数计算出的协方差矩阵，$\boldsymbol{I}$表示一个与$\boldsymbol{K}$维度相同的单位矩阵，$\eta$是衡量观察值噪声水平的常数。预期改进获取函数 $u(\boldsymbol{p})$衡量候选软提示相对于最佳soft prompt在目标值方面的改进，定义如下：

$u(\boldsymbol{p})=\mathbb{E}_{H(\boldsymbol{p}) \sim \mathcal{N}\left(\mu(\boldsymbol{p}), \sigma^2(\boldsymbol{p})\right)}\left[\max \left\{0, H(\boldsymbol{p})-\max _{i \in[m]} H\left(\boldsymbol{p}_i\right)\right\}\right]$

贝叶斯优化通过最大化$u(\boldsymbol{p})$来确定下一个soft prompt $p_{m+1}$进行探索：

$\boldsymbol{p}_{m+1} \in \underset{\boldsymbol{p} \in \mathbb{R}^d}{\operatorname{argmax}} u(\boldsymbol{p})$

在目标任务上两个指令zero-shot预测的相似性：

$s\left(v_i, v_j\right)=\mathbb{E}_{X \sim \mathcal{D}_t}\left[\operatorname{sim}\left(f\left(\left[v_i ; X\right]\right), f\left(\left[v_j ; X\right]\right)\right)\right],$

$\operatorname{sim}(\cdot,\cdot)$是预测结果（例如F1分数）的相似性，核函数(Matern or Squared Exponential kernels)在soft prompt和提示上分别对应两个核矩阵（$\boldsymbol{S},\boldsymbol{L}$），通过结合soft promt和指令的核函数进一步提出一个instruction-coupled kernel function：

$\boldsymbol{K}_{i, j}=k\left(\boldsymbol{p}_i, \boldsymbol{p}_j\right)=\boldsymbol{l}_i^{\top} \boldsymbol{L}^{-1} \boldsymbol{S} \boldsymbol{L}^{-1} \boldsymbol{l}_j$