总览
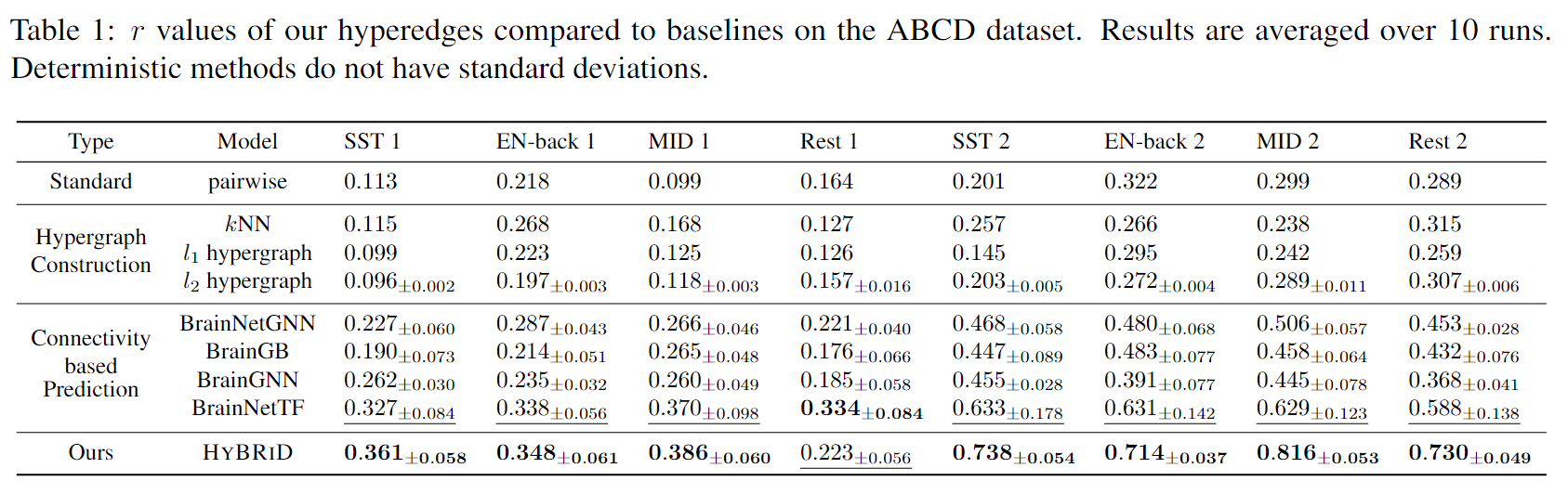
从fMRI信号中发现大脑区域之间可靠和信息丰富的关系对于表型预测至关重要。目前的大多数方法都无法准确表征这些相互作用,因为它们只关注成对连接而忽略了大脑区域的高阶关系。 高阶关系应该最大程度地提供信息和最小冗余。然而,由于指数搜索空间和缺乏易于处理的目标,识别这种高阶关系具有挑战性且尚未得到充分探索。本文提出了一种名为 HYBRID 的新方法,旨在从 fMRI 数据中提取 MIMR 高阶关系。HYBRID 采用 CONSTRUCTOR 来识别超边结构,WEIGHTER 计算每个超边的权重,从而避免在指数空间中搜索。HYBRID 通过创新的信息瓶颈框架实现了 MIMR 目标。模型在 CPM(一种研究大脑连接的标准协议) 测量的超边质量方面平均优于最先进的预测模型 11.2%。
背景
大脑功能可能涉及多个区域交互,信号通信可能对应高阶关系,高阶关系不一定适合分解成成对关系。因此,仅依靠成对连通性,而不考虑大脑复杂的高阶结构,可能会导致研究结果不一致,并且跨研究的预测性能较低。
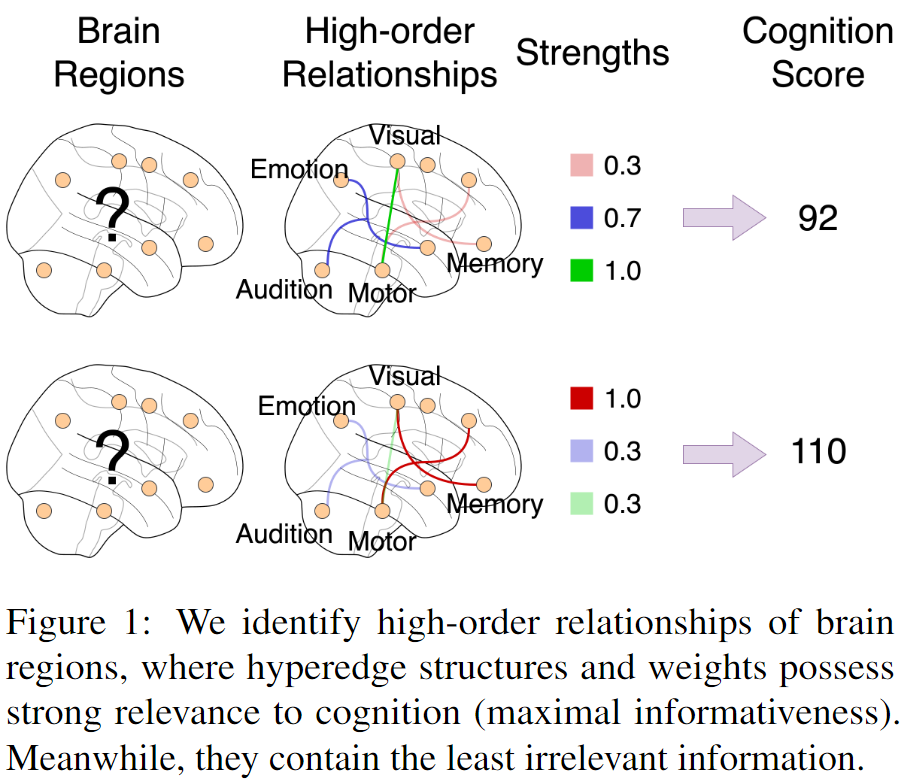
本文目标是确定对表型结果(如认知评分)有信息意义的高阶关系。然而,与成对关系不同,可能的高阶关系的数量是指数级的。为了从指数空间中识别出信息量最大的,我们提出了我们的目标:信息量最大、冗余度最小(MIMR)。也就是说,我们最大限度地利用高阶关系中包含的信息来获得神经结果(信息量),同时减少无关大脑区域的参与(冗余)。一方面,这样的标准确保了这些高阶关系的预测性能;另一方面,它赋予了模型识别更简洁和可解释结构的能力。将高阶关系表述为超图中的加权超边,其中区域被视为节点。与边只连接两个节点的传统图不同,超图允许边,称为超边,连接任意数量的节点。超图应该加权,超边的权重被认为是高阶关系的优势,其中包含与结果相关的信息(图 1)。
然而,目前的超图构造方法大多基于邻居距离和邻居重构,不适合本文上下文,原因如下:1)由于缺乏学习这种超边的可处理目标,无法学习MIMR超边。2)不能跨受试者学习一致的结构,这认知功能机制应该相似的信念相矛盾。3)超边的数量被限制在节点的数量上,可能会导致次优性能。此外,尽管信息瓶颈(IB)一直是深度学习中学习MIMR表示的主流解决方案,现有的IB方法专注于提取输入的压缩表示,而不是识别底层结构,如超图。
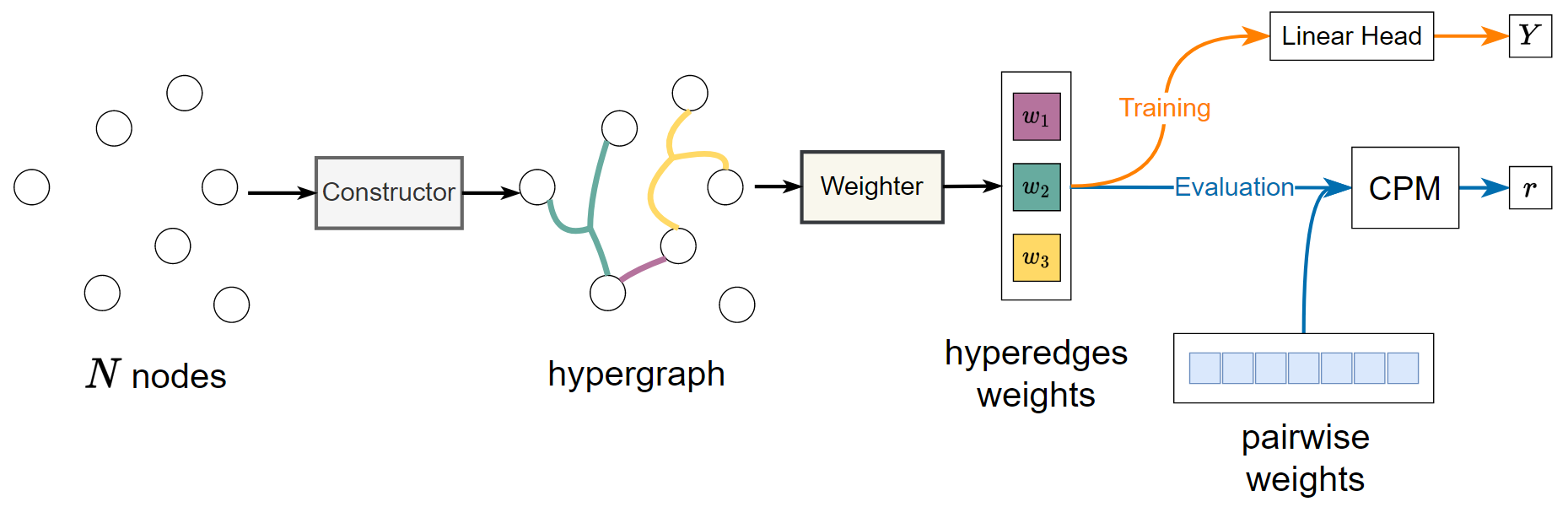
本文提出HYBRID,HYBRID的整体流程如图所示。HYBRID包含CONSTRUCTOR和WEIGHTER。CONSTRUCTOR通过学习掩码集来识别大脑区域的超边结构,WEIGHTER为每个超边计算一个权重。进一步提出multi-head drop-bottleneck并推导出其优化目标。HYBRID通过学习掩码来识别超边界,避免了在指数空间中搜索,从而保证了效率。其与特征无关的掩蔽机制设计确保了HYBRID能够学习跨受试者的一致结构。此外,该模型配备了多个平行头,每个头都专用于一个超边。通过这种方式,HYBRID能够识别任意数量的超边,具体取决于它的头数量 。
问题定义和符号
数据集包含人类受试者特征和表型结果,由对表示。是矩阵,是区域数量,是特征维度,特征是从fMRI时间序列中得出的Pearson相关性。,表示表型结果,如智商。基于输入X,HYBRID目标是学习一个大脑的加权超图,包括超边集合和边权重集合。将超边和节点联系起来:
是一个由0和1组成的维mask向量。
相关工作
Hypergraph Construction
现有的超图构造方法大多基于neighbor reconstruction和neighbor distances,超边数量受限于节点数,无法学习MIMR超边,还有基于属性的方法,需要离散的标签,不适用本文。
High-Order Relationships in fMRI
现有的在fMRI构造超图的方法存在局限,比如非学习的方法表达力不够,有噪声,列举度数小于3的超边扩展性不行等等。
Information Bottleneck
IB是一种信息压缩技术,核心思想是提取数据中与目标最相关的信息,先前的工作一般是用于抽取压缩的表示或者特征,本文侧重识别数据的底层结构。
Connectivity-based Phenotypic Prediction
根据大脑区域连通性预测表型结果,一般把大脑网络建模为图的话,区域作为节点,两个节点之间的相关性作为边,主要通过GNN捕获连接信息进行预测。
方法
HYBRID由CONSTRUCTOR WEIGHTER LINEARHEAD 组成:
超边数量是超参,每条超边都会分配一个头来选择该边的相关节点,即输出列向量,每一项是一个可学习的概率再套一个指示函数。但是指示运算没有梯度,所以使用stop-gradient技术进行近似。
超边的权重通过Readout模块获得,该模块(1)对所有非mask节点特征求和(2)降维:
DimReduction是通过MLP和ReLu,权重会被输入最终线性层预测标签。
由于没有现有的IB框架可以应用,本文提出multi-head drop-bottleneck,从IB的角度把,,作为马尔科夫链中的随机变量,根据MIMR目标,优化
第一项代表信息量,第二项代表冗余。由于优化高维连续变量的互信息是棘手的,改为优化该方程的下限,展开第一项:
可以看成是的函数组合,可以被作为一个方差为1的高斯模型。
(将 设为方差为1的高斯模型,意味着在实际应用中,我们假设 在给定 后的分布是一个高斯分布,且这个分布的方差被固定为1。高斯分布是连续数据建模中常用的分布,因为它具有良好的数学性质,如可微性和封闭形式的解。方差为1的高斯分布意味着我们假设预测的不确定性是标准化的,这有助于模型的泛化能力。在概率机器学习模型中,使用高斯分布来建模连续数据是一种常见的做法,因为它允许我们利用高斯分布的性质来简化计算和优化过程。例如,高斯分布的对数似然函数是可微的,这使得我们可以使用梯度下降等优化算法来调整模型参数 ,以最小化预测误差。此外,高斯分布的参数(均值和方差)可以直接从数据中估计,这使得模型训练过程更加直观和易于实现。)
再来看看冗余的上界:
最终的损失函数为:
实验
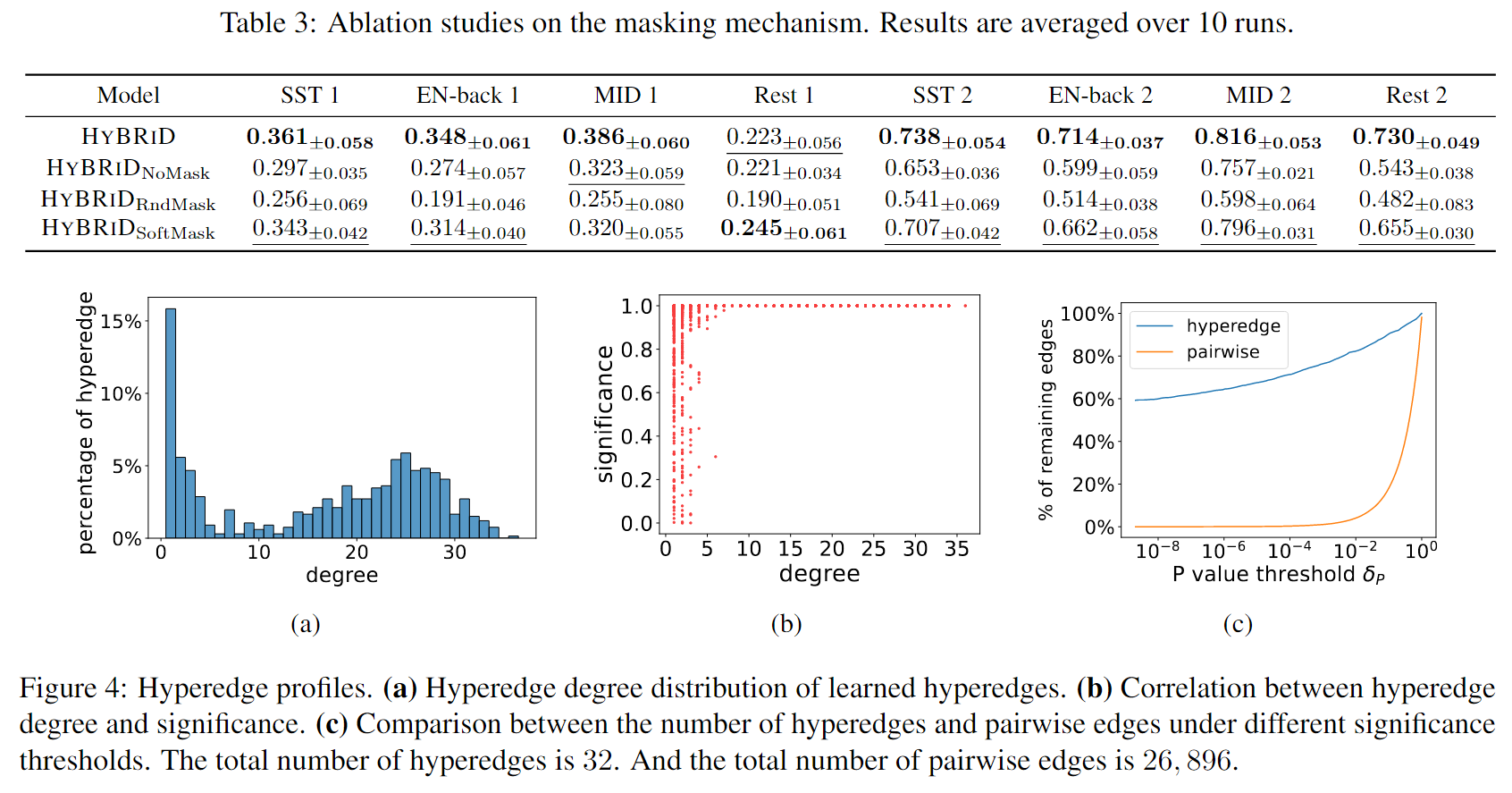
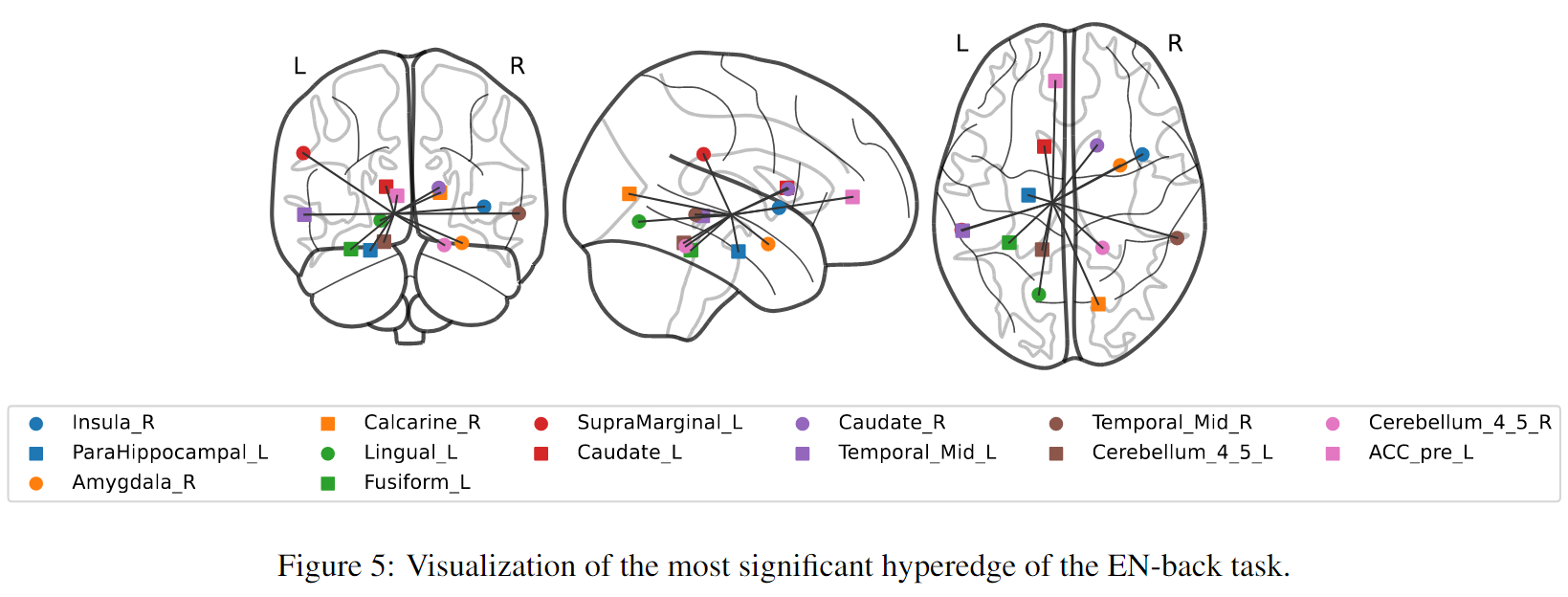
解释下b图,由于CPM基于线性回归模型在内部对成对边和超边进行了显著性检验(详见附录B),可以从显著性检验中获得每个超边的P值。定义超边的显著性为1-p值,在这个图中,发现超边缘的程度与其重要性之间存在很强的正相关关系,这表明多个大脑区域的相互作用在认知中比成对或单个区域的作用更重要。