一、总结

1. 这篇论文要解决什么问题？

众所周知，全局注意力机制在全连通图中考虑了更宽的感受野，导致许多人相信可以从所有节点中提取有用的信息。本文通过展示经验证据和理论分析来揭示 Graph Transformer 中的过度全局化问题，即当前的注意力机制过度关注那些遥远的节点，而实际上包含大部分有用信息的近节点相对减弱。本文提出了一种新的具有协作训练的双层全局图变换器（CoBFormer），包括簇间和簇内变换器，以防止过度全球化问题，同时保持从远程节点提取有价值信息的能力。此外，提出了协同训练，在理论保证下提高了模型的泛化能力。

2. 已有工作的思路以及不足之处有哪些？

图神经网络存在过度平滑和过度挤压问题，限制了它对临近节点的感受野。实证发现，所有节点对的学习注意力得分分布与实际信息节点的分布之间存在不一致，即全局注意力机制倾向于关注高阶节点，而有用信息通常出现在低阶节点。现在有一类主要方法是结合GNN作为局部信息模块跟Graph Transformer 结合，GNN中局部平滑和图变换器中过度全球化的不同特性提出了一个基本问题，即哪些信息将主要影响节点表示，只是线性组合存在比单独用局部或者全局信息更差的情况。

3. 作者的洞见（insight）有哪些？

从实验上发现和理论上证明了Graph Transformer 在节点分类上存在过度全局化问题。

4. 解决方法的基本思想是什么？

本文提出了一种新的具有协同训练的双层全局图变换器（CoBFormer）。具体来说，首先使用METIS算法将图划分为不同的簇。随后，引入双层全局注意力（BGA）模块，该模块由簇内Transformer和簇间Transformer组成。该模块通过解耦簇内和簇间的信息，缓解了过度全局化问题，同时保持了全局感受能力。为了捕获BGA模块忽略的图形结构信息，采用图形卷积网络（GCN）作为局部模块。最后，提出了协作培训，以整合GCN和BGA模块学习到的信息，提高其性能。

二、过度全局化问题

经验观察

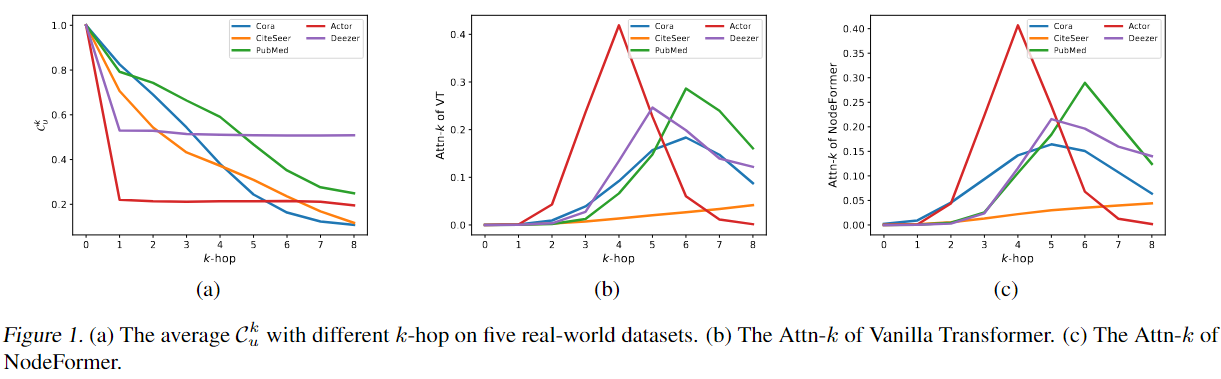
将具有与节点uu相同标签的kk跳邻居（因为是节点分类任务，所以标签相同的节点更有帮助）的比例定义为：

Cuk=∣v∈Nk(u):yu=yv∣∣Nk(u)∣\mathcal{C}_u^k=\frac{\left|v \in \mathcal{N}^k(u): \mathbf{y}_u=\mathbf{y}_v\right|}{\left|\mathcal{N}^k(u)\right|}

其中Nk(u)\mathcal{N}^k(u)表示节点uu的第kk跳邻居。与kk跳邻居相关的平均注意力分数：

Attn-k=Eu∈V∑v∈Nk(u)αuv.\text {Attn-} k=\mathbb{E}_{u \in \mathcal{V}} \sum_{v \in \mathcal{N}^k(u)} \alpha_{u v} . 

注：Homophilic Graph（同配图） 和 Heterophilic Graph（异配图） 是根据图中节点连接模式对图进行分类的两种类型。它们的主要区别在于节点连接的偏好性：
Homophilic Graph（同配图）
在同配图中，节点倾向于与具有相似特征、属性或标签的其他节点相连。例如，在社交网络中，具有相似兴趣爱好或背景的人更可能成为朋友。这种图的连接模式通常表现出较高的同质性，即相似的节点聚集在一起。
同配图的一个典型特点是图中存在大量的对称邻域结构，节点的邻域信息可以很好地反映其自身的属性。
图神经网络（GNN）通常在同配图上表现良好，因为它们可以利用节点间的相似性来聚合信息。
Heterophilic Graph（异配图）
在异配图中，节点倾向于与具有不同特征、属性或标签的其他节点相连。例如，在生物网络中，不同类型的氨基酸通过化学键连接，形成复杂的蛋白质结构。
异配图的连接模式较为复杂，节点的邻域信息可能包含大量异质性信息，这使得传统的基于同配假设的图神经网络方法难以有效处理。
异配图的一个挑战是节点的连接模式不遵循同配图中的对称性，因此需要设计更复杂的模型来捕捉节点间的异质性。
总结来说，同配图和异配图的主要区别在于节点连接的偏好性：同配图中相似节点相连，而异配图中不同节点相连。这种差异对图神经网络的设计和应用产生了重要影响。

图1a展示了三个同配图（Homophilic Graph）和两个异配图（Heterophilic Graph），可以看到，同配图通常随着kk增加而Cuk\mathcal{C}_u^k减小，而异配图在1跳时就急剧减小，随后保持几乎不变。这表明同配图从节点分类的局部结构中受益更多，而异配图从全局感受野中获得更多信息。然后，可视化Vanilla Transformer（VT）和NodeFormer的Attn−kAttn-k，以检查Attn−kAttn-k的趋势是否与图1（a）一致。为了实现这种可视化，取每个头部的平均注意力得分，并绘制第一层的结果（后续层将呈现类似的趋势）。如图1（b）和1（c）所示，大多数注意力得分实际上都分配给了遥远的高阶邻居，无论这些图是同配图还是异配图。将这种现象确定为Graph Transformers中的过度全局化问题，强调全局注意力机制的局限性。

理论分析

理想情况下，Graph Transformers能给相似嵌入分配更高的嵌入分数，隐式学习到一个邻居节点嵌入平滑的图结构。因此，$$||Z-\hat{A}Z||_F$$应该相对比较小。这里ZZ表示节点嵌入，所以使用$$||Z-\hat{A}Z||_F$$评估Graph Transformer学到邻居节点嵌入的平滑性。Cu\mathcal{C}_u表示节点uu的可到达集合中与其属于同一类的比例。如果uu的可到达集合是在KK跳以内，那么Cu\mathcal{C}_u可以表示为：

Cu=∑k=0KCuk∣Nk(u)∣∑k=0K∣Nk(u)∣\mathcal{C}_u=\frac{\sum_{k=0}^K\mathcal{C}_u^k|\mathcal{N}^k(u)|}{\sum_{k=0}^K|\mathcal{N}^k(u)|}

下面建立∣∣Z−A^Z∣∣F||Z-\hat{A}Z||_F、αuv\alpha_{uv}、Cu\mathcal{C}_u联系：

定理3.1 对于一个给定节点uu和一个训练良好的Graph Transformer，定义ηu=Ev∈V,yu=yvexp⁡(qukvTd)\eta_u= \mathbb{E}_{v \in \mathcal{V}, y_u = y_v} \exp\left(\frac{\mathbf{q}_u \mathbf{k}_v^T}{\sqrt{d}}\right)，$ \gamma_u = \mathbb{E}_{v \in \mathcal{V}, y_u \neq y_v} \exp\left(\frac{\mathbf{q}_u \mathbf{k}_v^T}{\sqrt{d}}\right)$。然后，我们有：

∥Z−A^Z∥F≤2L∑u∈V∑v∈V,yu≠yvαuv=2L∑u∈V11+Cu1−Cuηuγu\|Z - \hat{A}Z\|_F \leq \sqrt{2}L \sum_{u \in \mathcal{V}} \sum_{v \in \mathcal{V}, y_u \neq y_v} \alpha_{uv} = \sqrt{2}L \sum_{u \in \mathcal{V}} \frac{1}{1 + \frac{\mathcal{C}_u}{1 - \mathcal{C}_u} \frac{\eta_u}{\gamma_u}}

其中LL是一个Lipschitz常数。

**证明：**为了证明定理3.1，假设存在一个由WCW_C参数化的线性分类器，满足条件ZWC=YZW_C = Y，这意味着Z=YWC−1Z = YW_C^{-1}。

∥Z−A^Z∥F=∥∑u∈V(zu−∑v∈Vαuvzv)∥2\|Z - \hat{A}Z\|_F = \|\sum_{u \in \mathcal{V}}(z_u - \sum_{v \in \mathcal{V}} \alpha_{uv} z_v)\|_2

\begin{equation} \begin{aligned} \| \mathbf{Z} - \mathbf{\hat AZ} \|_F &\le \sum_{u \in \mathcal{V}} \| \mathbf{z}_u - \sum_{v \in \mathcal{V}} \alpha_{uv}\mathbf{z}_v \|_2 &&\cdots \sqrt{a+b+c}\le\sqrt{a} + \sqrt{b} + \sqrt{c} \\ &= \sum_{u \in \mathcal{V}} \|\sum_{v \in \mathcal{V}} \alpha_{uv}(\mathbf{z}_u-\mathbf{z}_v) \|_2 &&\cdots \sum_{v \in \mathcal{V}} \alpha_{uv}=1 \\ &\le \sum_{u,v \in \mathcal{V}} \alpha_{u,v} \| \mathbf{z}_u-\mathbf{z}_v \|_2 &&\cdots \text{The Triangle Inequality} \\ &\le L\sum_{u,v \in \mathcal{V}} \alpha_{u,v} \| \mathbf{y}_u-\mathbf{y}_v \|_2 &&\cdots \text{Lipschitz Continuous} \\ &= L\sum_{u \in \mathcal{V}}\sum_{v \in \mathcal{V},y_v = y_u} \alpha_{u,v} \| \mathbf{y}_u-\mathbf{y}_v \|_2 + L\sum_{u \in \mathcal{V}}\sum_{v \in \mathcal{V},y_v \ne y_u} \alpha_{u,v} \| \mathbf{y}_u-\mathbf{y}_v \|_2 \\ &= \sqrt{2}L\sum_{u \in \mathcal{V}}\sum_{v \in \mathcal{V},y_v \ne y_u} \alpha_{u,v}. \end{aligned} \end{equation}

所以定义3.1展示了$$||Z-\hat{A}Z||_F$$的边界与Cu\mathcal{C}_u负相关。同时发现Cuk\mathcal{C}_u^k的一些属性：


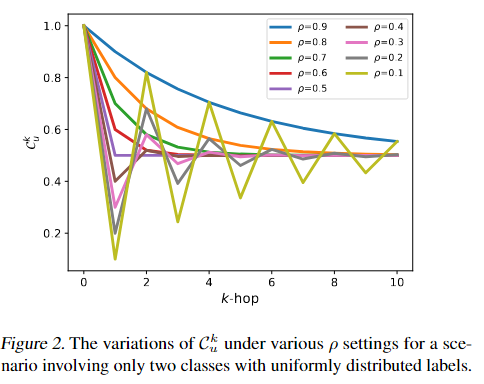
接下来提出注意力信噪比，利用Cora和Citseeer上的Attn信噪比和准确性来评估Vanilla Transformer和NodeFormer。

只要对相同的标签的节点注意力成倍，效果就会显著提升。

三、方法

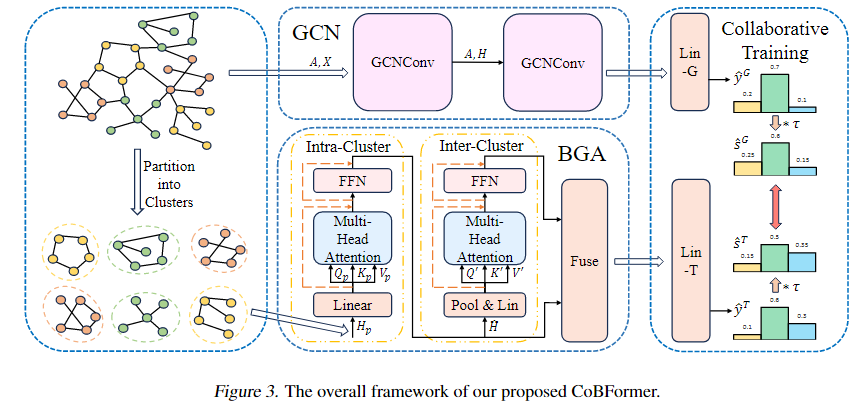
双层全局注意力模块

首先通过METIS将图划分为P个不重叠的簇。每个簇的节点特征会被输入给intra-cluster Transformer，输出簇表示。然后簇表示再输入inter-cluster Transformer。通过解耦簇内信息和簇间信息，可以缓解过度全局化问题，同时保留全局注意力的能力。

协同训练

以前工作，模型训练只依赖有标签节点训练交叉熵，但是这种方法不能保证在无标签节点的性能。所以本文提出了一种协同训练方法，鼓励BGA模块在未见节点预测的软标签监督GCN模块，反之亦然。通过相互监督，GCN和BGA模块可以从对方的错误中学习，从而提高模型对未标记数据的泛化能力。这种协同效应有助于模型在面对新的、未见过的数据时，能够做出更准确的预测。