一、总结
1. 任务介绍
本研究旨在通过分析功能磁共振成像(fMRI)时间序列的拓扑特征,对轻度认知障碍(MCI)及其亚型(早期MCI, EMCI;晚期MCI, LMCI)进行分类,并探索其与健康对照组(HC)的神经生物学差异。研究重点关注六个经典脑网络的160个ROI(感兴趣区域),利用拓扑数据分析工具(持续同调)和深度学习模型,揭示MCI不同阶段的脑功能连接拓扑变化。
2. 解决什么问题?
- 临床挑战:MCI是阿尔茨海默病(AD)的前驱阶段,但其亚型(EMCI/LMCI)的早期诊断困难,传统基于记忆评分的分类特异性低,易误判。
- 科学问题:MCI亚型向AD转化的风险差异显著,但缺乏敏感的生物标志物来量化其脑功能拓扑变化。
- 技术目标:开发一种新方法,通过拓扑特征捕捉MCI亚型与HC的细微差异,提升分类准确性,为早期干预提供依据。
3. 最朴素的(传统)做法是什么?
传统方法主要依赖基于机器学习和深度学习的特征工程,例如:
- 使用MRI模态(如结构/功能MRI)提取静态功能连接特征(如相关系数、图论指标)。
- 直接利用时间序列的统计特征(如均值、方差)或频域特征进行分类。
局限性:可能忽略动态功能连接的拓扑结构变化,难以捕捉MCI亚型间细微的时空模式差异。
4. 本文的做法与创新
方法:
- 拓扑特征提取:
- 将每个ROI的fMRI时间序列通过滑动窗口嵌入转换为三维向量序列。
- 计算各维度(0维、1维、2维)的持久图(Persistence Diagrams, PDs),量化拓扑特征(如连通性、环状结构)。
- 使用Wasserstein距离度量拓扑差异。
- 分类模型:提出新的深度学习模型,结合拓扑特征进行分类。
解决的问题:
- 传统方法无法捕捉动态功能连接的拓扑演化。
- 通过持久同源性揭示不同MCI亚型的脑网络拓扑退化模式。
创新点:
- 首次将持久同源性应用于fMRI时间序列,分析MCI亚型的拓扑特征差异。
- 提出“ROI特异性跨被试”和“被试特异性跨ROI”两种交互分析模式,全面量化拓扑变化。
- 结合TDA与深度学习,显著提升分类性能(ADNI数据集准确率95%,内部数据集85%)。
5. 实验发现与洞察
实验结果:
- 分类性能:
- ADNI数据集:HC vs. MCI准确率95%,内部数据集85%。
- 亚型分类:HC vs. EMCI(76.5%)、HC vs. LMCI(91.1%)、EMCI vs. LMCI(80%)。
- 关键发现:
- LMCI相比HC和EMCI,在多个脑网络(如默认网络、注意网络)中表现出显著的拓扑退化(如连通性降低、环结构减少)。
- EMCI的拓扑变化更细微,主要集中于记忆相关网络(如海马区域)。
理论洞察:
- 脑功能网络的拓扑稳定性(如高维Betti数)与认知衰退程度相关,可能作为疾病进展的生物标志物。
- 不同MCI亚型的拓扑退化模式反映了疾病阶段的异质性,支持“EMCI→LMCI→AD”的病理发展假说。
6. 改进方向与扩展性
改进方向:
- 多模态融合:结合结构MRI、弥散张量成像(DTI)或生物标记物(如Aβ蛋白),提升分类鲁棒性。
- 动态拓扑分析:引入时间序列的动态网络分析(如时变持久同源性),捕捉更精细的时空演化模式。
- 模型可解释性:通过注意力机制或显著性映射,解释深度学习模型依赖的拓扑特征。
扩展性:
- 其他神经系统疾病:如帕金森病、精神分裂症,其功能网络也可能存在特异性拓扑退化。
- 纵向研究:追踪拓扑特征随时间的变化,预测MCI向AD的转化风险。
待解决问题:
- 数据异质性:不同扫描设备或协议的跨数据集泛化能力需验证。
- 计算效率:TDA的高计算复杂度可能限制大规模应用,需优化算法。
7.数据和代码
代码:https://github.com/blackpearl006/ICPR-2024
二、方法
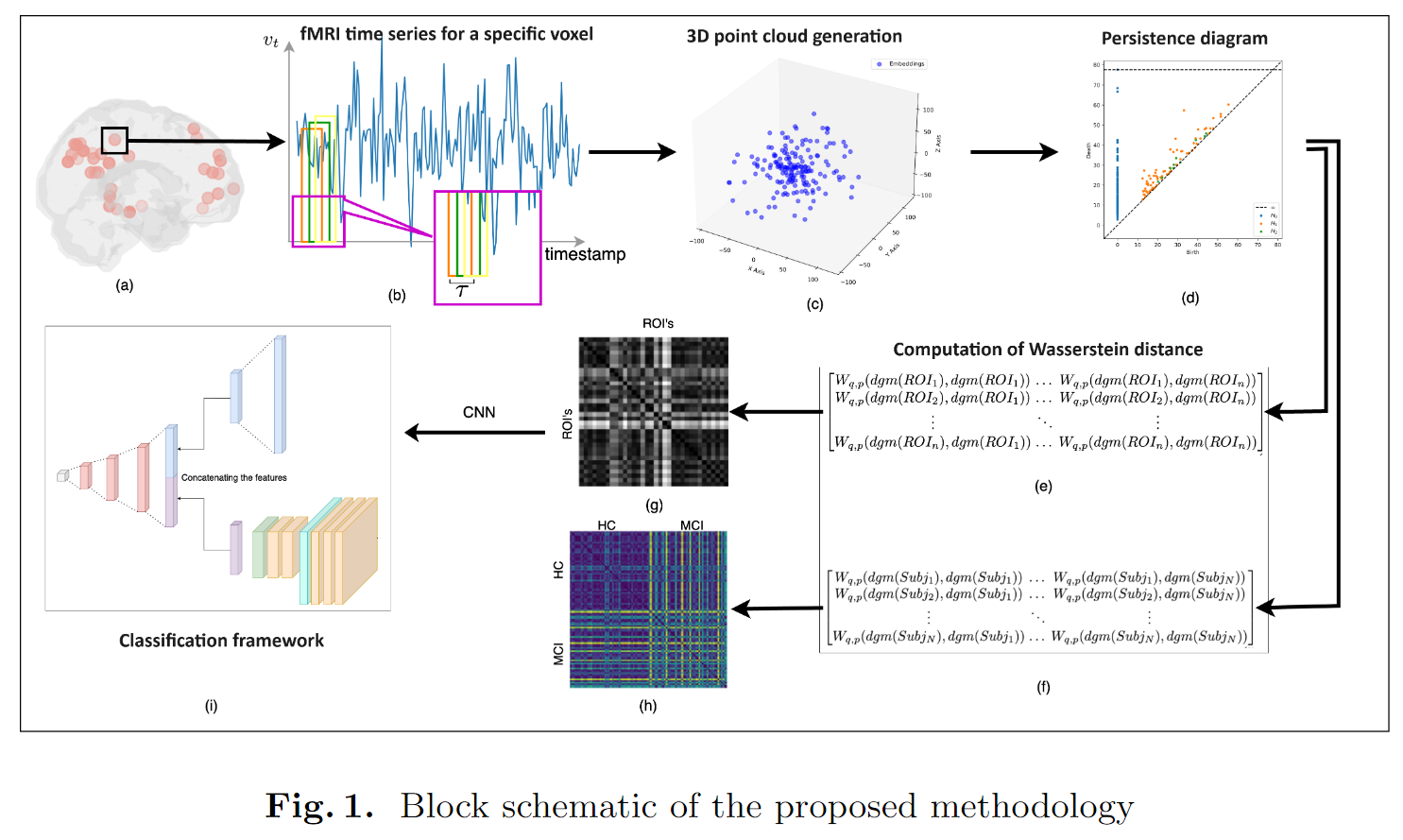
工作流:一维fMRI时间序列数据→三维点云→持续性图(persistence diagram)→Wasserstein距离计算所有可能的持续性图对(量化拓扑变化)→给定ROI的受试者之间拓扑变化和给定受试者的ROI之间的拓扑变化
抽取时间序列
根据Dosenbach 160图谱划分的ROI提取脑区的fMRI时间序列。Dosenbach's ROI分为六个脑网络:小脑(cerebellum,n=18),带状盖(cingulo-opercular,n=32),默认模式(default mode,n=34),额顶叶(fronto-parietal,n=21),枕叶(occipital,n=22)和感觉运动(sensorimotor,n=33)网络。这些大脑网络中的每一个都与特定的认知、感觉和运动功能有关,并可能在MCI的不同阶段表现出独特的破坏模式。因此,通过分析所有六个网络,该研究提供了对网络特定变化的全面评估,这些变化可以作为不同阶段或类型认知障碍的不同生物标志物。
从时间序列中构建点云
在这一步中,目标是构建一个更丰富的特征空间,以分析MCI内在拓扑特性的变化。时间序列中的每个点都映射到3D空间中的一个向量,以捕捉复杂的时间动态(图1.C)。使用一个嵌入维度和时间间隔的滑动窗口嵌入将时间序列转换为点云。滑动窗口长度设置为,以尽量减少噪声干扰和更好的可解释性。一个基于的函数的滑动窗口嵌入表示为:
所以,选择不同的值会产生一个点集,也就是函数(fMRI时间序列数据本身,即fMRI时间序列的值随时间的变化关系)的滑动窗口点云。在这项研究中,对于嵌入维数,fMRI时间序列的点云表示为:
点云中每个点都是一个三维向量,与fMRI数据的空间维度一致。
持续同调
接下来要从生成的3D点云中计算持续同调,以提取不同维度的拓扑特征。使用Vietoris-Rips过滤构建一系列单纯复形(Simplicial Complex)并计算它们的同调特征来实现的。这些特征捕捉了数据中的底层拓扑结构,识别了MCI及其子类型之间有意义的模式和差异。利用持续性图编码的信息来分析MCI患者和HC患者大脑网络拓扑结构的差异。
持续性图将过滤参数范围内数据中的持续性特征编码为二维欧式空间中的点集合。从点云构建过滤的一种常见方法是通过Vietoris-Rips复形,连接成对距离在指定阈值内的任何点子集,从点云中生成的,从而创建一个单纯形。因此,过滤是空间集合,其中 $ F_\epsilon \subset F_{\epsilon'} $ 对于所有 $ \epsilon \leq \epsilon' $ 成立。的第个持续图是一个多集,每个对编码了一个维拓扑特征,换句话说Betti描述符与一个在处出生并在处死亡的单纯形复数相关联。是特征的持久性,通常用于衡量整个过过滤程中的重要性。给定一个时间序列 ,计算滑动窗口点云$SW_{M, \tau} f $,该点云位于度量空间 中。Rips过滤 $ VR(X, M_X) $ 是从Vietoris-Rips复形 $ VR_\epsilon(X, M_X) $ 派生而来,计算在每个尺度 $ \epsilon \geq 0 $上。Rips过滤的数学表达式在公式:
其中
这表示在尺度 $\epsilon $ 下,所有点对之间的最大距离小于 $ \epsilon $ 的点集。Rips持久图中的出生-死亡对 $ (b, d) $ 揭示了空间 的底层拓扑结构。在 $ dgm_i^{VR}(X) $ 中具有大持久值 $ (d - b) $ 的点 $ (b, d) $ 表明了连续空间中 $ X $ 集中的最持久的拓扑特征。
Wasserstein距离用于衡量两个fMRI时间序列之间的相似性。低Wasserstein距离表明两个fMRI时间序列在时间上表现出相似的神经活动模式,这意味着这两个脑区在功能上是同步的,可能参与协调活动。相反,高Wasserstein距离表明两个脑区的fMRI时间序列具有不同的神经活动模式,可能是功能上分离或独立的。高Wasserstein距离还可能表明两个脑区之间的功能连接存在异常,这可能是任何神经或精神疾病的迹象。
持久性图是拓扑数据分析中的一种工具,用于编码数据在不同尺度下的拓扑特征。它通过记录特征(如连通分量、洞等)的出现(birth)和消失(death)来捕捉数据的拓扑结构。给定两个不同的过滤(filtrations)$ f_1 $ 和 $ f_2 $,以及对应的持久性图 $ X = dgm_p(f_1) $ 和 $ Y = dgm_p(f_2) X $ 和 $ Y $ 之间的不相似性。$ L_\infty(f_1, f_2) = |f_1 - f_2|_\infty $ 表示 $ f_1 $ 和 $ f_2 $ 之间的最大距离。$ \eta $ 表示从 $ X $ 到 $ Y $ 的一个双射,即一一对应关系。-Wasserstein距离定义为:
这个公式表示在所有可能的双射 $ \eta $ 下,找到使总距离最小的那个双射,并计算对应的Wasserstein距离。首先,对于 $ X $ 中的每个元素 $ x $ 和 $ Y $ 中对应的元素 $ y = \eta(x) $,计算它们之间的差异(成本函数),使用 $ |x - \eta(x)|\infty $,即 $ L\infty $ 范数。将这些差异的 $ q $ 次幂相加,得到整个多集 $ X $ 和 $ Y $ 在匹配 $ \eta: X \rightarrow Y $ 下的差异。在所有可能的双射 $ \eta $ 上取下确界(infimum),得到在最佳匹配下 $ X $ 和 $ Y $ 之间的差异,从而有效地消除了 $ \eta $ 的进一步考虑。瓶颈距离是Wasserstein距离的一个特例,当参数 $ q \rightarrow \infty $ 时。瓶颈距离的一个缺点是它对双射中超出最远对应点对的细节不敏感。
在这里,持久性图是为两种不同场景计算的:
- ROI-specific:针对特定个体的所有ROI。
- Subject-specific:针对特定ROI的所有考虑的HC和MCI个体。
因此,使用Wasserstein距离 $ W_{q, p}(X, Y) $ 来衡量所有ROI之间以及所有个体之间的成对距离。
特定ROI跨被试变化
-
目的:理解所有考虑的个体中,对于每个Betti描述符(),拓扑模式的相似性。
-
方法:使用Wasserstein距离来衡量不同个体的持久性图之间的距离。
-
表示:这些距离被表示在一个成对个体距离矩阵(PS)中,其维度为 ,其中 是个体的数量。
-
数学表示:矩阵 的每个元素 表示特定脑网络的给定ROI中,个体 和个体 的持久性图之间的Wasserstein距离。
-
计算:计算这些距离需要高性能计算(HPC)资源,因为计算持久同调和Wasserstein距离矩阵( 和 )非常耗时。
-
PS矩阵:
特定被试跨ROI变化
-
目的:对于每个Betti描述符(),计算不同ROI之间的交互。
-
方法:同样使用Wasserstein距离来衡量不同ROI的持久性图之间的距离。
-
表示:这些距离被表示在一个成对ROI距离矩阵(PR)中,其维度为 ,其中 是特定脑网络的ROI数量。
-
数学表示:矩阵 的每个元素 表示ROI 和ROI 的持久性图之间的距离。
-
计算:同样,计算这些距离需要高性能计算资源,因为计算过程非常耗时。
-
PR矩阵:
分类
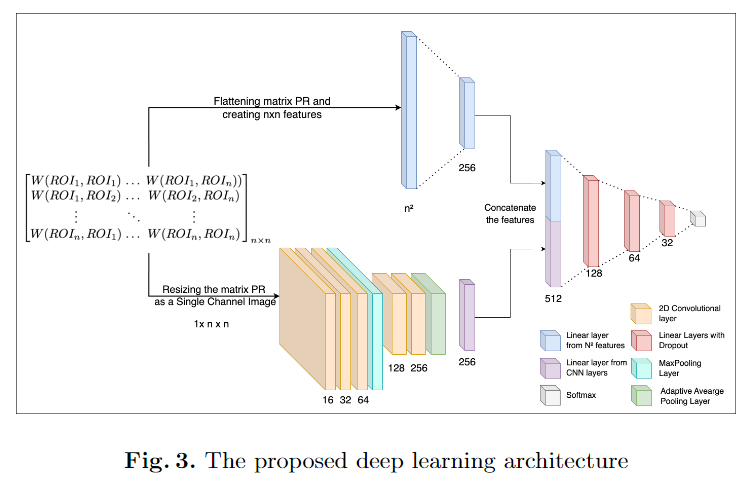
使用基于CNN的分类框架,整合从Wasserstein距离矩阵中提取的1D和2D特征。
数据和特征提取
- 数据:使用特定于个体的PR矩阵(),其中是特定脑网络的ROI数量。
- 特征提取:
- 1D特征:通过将Wasserstein距离矩阵展平来创建,关注成对关系。
- 2D特征:通过CNN层从距离矩阵中提取,以捕获局部模式和空间层次结构。
CNN架构
-
架构:提出的CNN模型包括两个步骤:
- 将Wasserstein距离矩阵展平以创建1D特征。
- 通过CNN层从距离矩阵中提取2D特征。
-
特征整合:将展平矩阵的特征和CNN层的特征连接起来,创建一个统一的特征向量,结合了线性和卷积层的信息。
分类过程
- 特征处理:连接的特征通过几个带有dropout的密集层进行正则化,以减少过拟合的风险。
- 特征优势:结合1D和2D特征允许模型创建更丰富和多样化的特征空间,可以捕获数据的不同方面。
CNN层细节
- CNN层:模型包括三个CNN层,分别有16、32和64个滤波器,随后是一个最大池化层和另一个包含128和256个滤波器的卷积块。
- 内核大小:所有CNN层使用3的内核大小。
- 全局平均池化层:将每个特征图压缩成一个单一值,形成一个线性特征向量。
- 激活函数:整个模型中使用ReLU激活函数。
1D特征处理
- 线性层:PR矩阵的1D特征()通过一个线性层处理,减少到256个特征。
- 特征向量:这个线性层产生的256维特征向量和2D CNN的256维特征向量被连接,并作为一系列全连接层的输入。
分类层
- 全连接层:大小为128、64和32,每个都包含设置为0.2的dropout。
- 激活函数:最终层使用softmax激活函数进行分类。
训练和评估
- 训练:模型使用Adam优化器进行100个周期的训练,学习率为0.001,训练-测试分割为80-20。
- 损失函数:使用交叉熵损失进行训练。
- 分类场景:模型被训练来分类以下场景:(i) MCI与HC(对于ADNI和内部数据集),(ii) EMCI与HC(ADNI),(iii) LMCI与HC(ADNI),以及(iv) EMCI与LMCI(ADNI)。
实验环境
- 硬件:使用2×16GB NVIDIA Tesla T4 GPU。
- 软件:使用Kaggle notebook和PyTorch深度学习框架进行实验。
总结来说,这项研究通过整合1D和2D特征,使用CNN模型来区分MCI的不同阶段,展示了持久同调在医学诊断中的潜力。通过结合不同层次的特征,模型能够更全面地理解和分类数据,从而提高分类的准确性和可靠性。
三、实验
特定ROI的不同组受试者Wasserstein距离()差异:
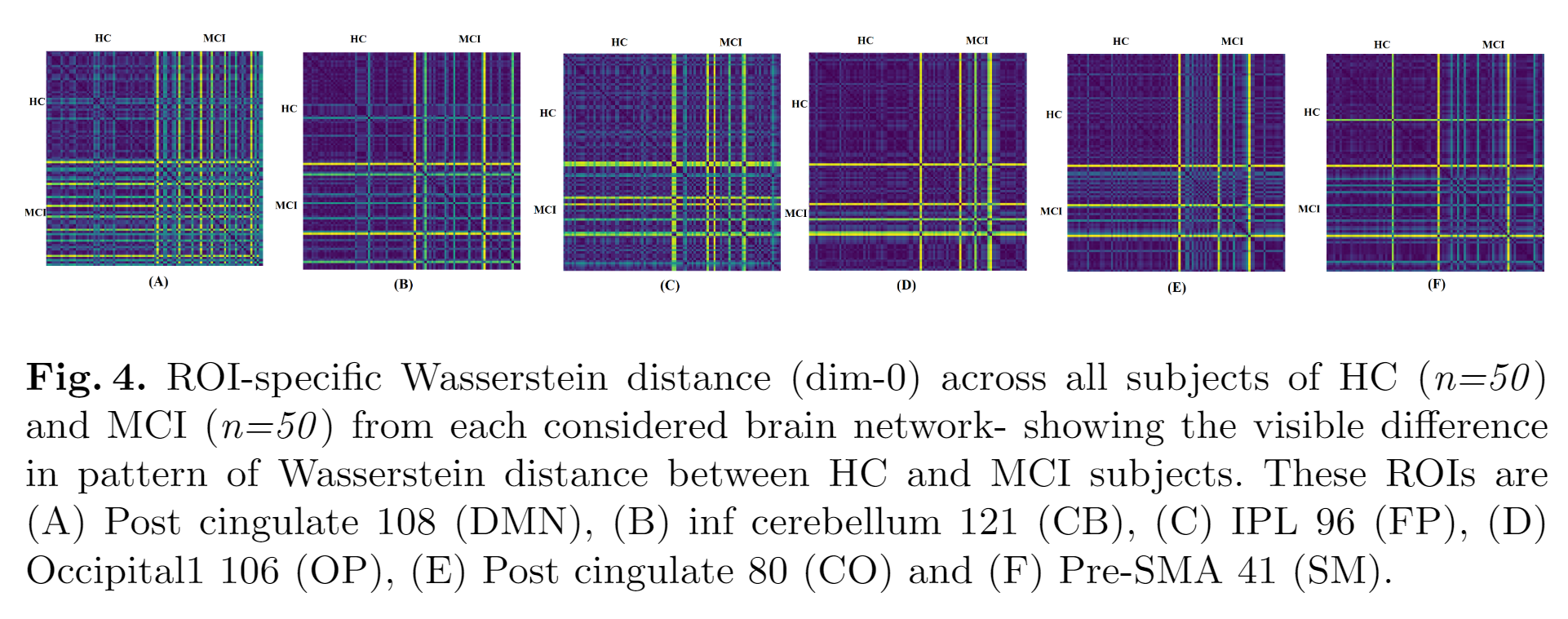
EMCI和LMCI的默认模式网络的P图可视化(99%置信区间),后3列突出显示了ROI对(与HC组比较)(P<0.01)。这与EMCI相比,可能表明在LMCI中,随着同调维度的增加,脑网络的拓扑结构变化集中在更少的脑区。

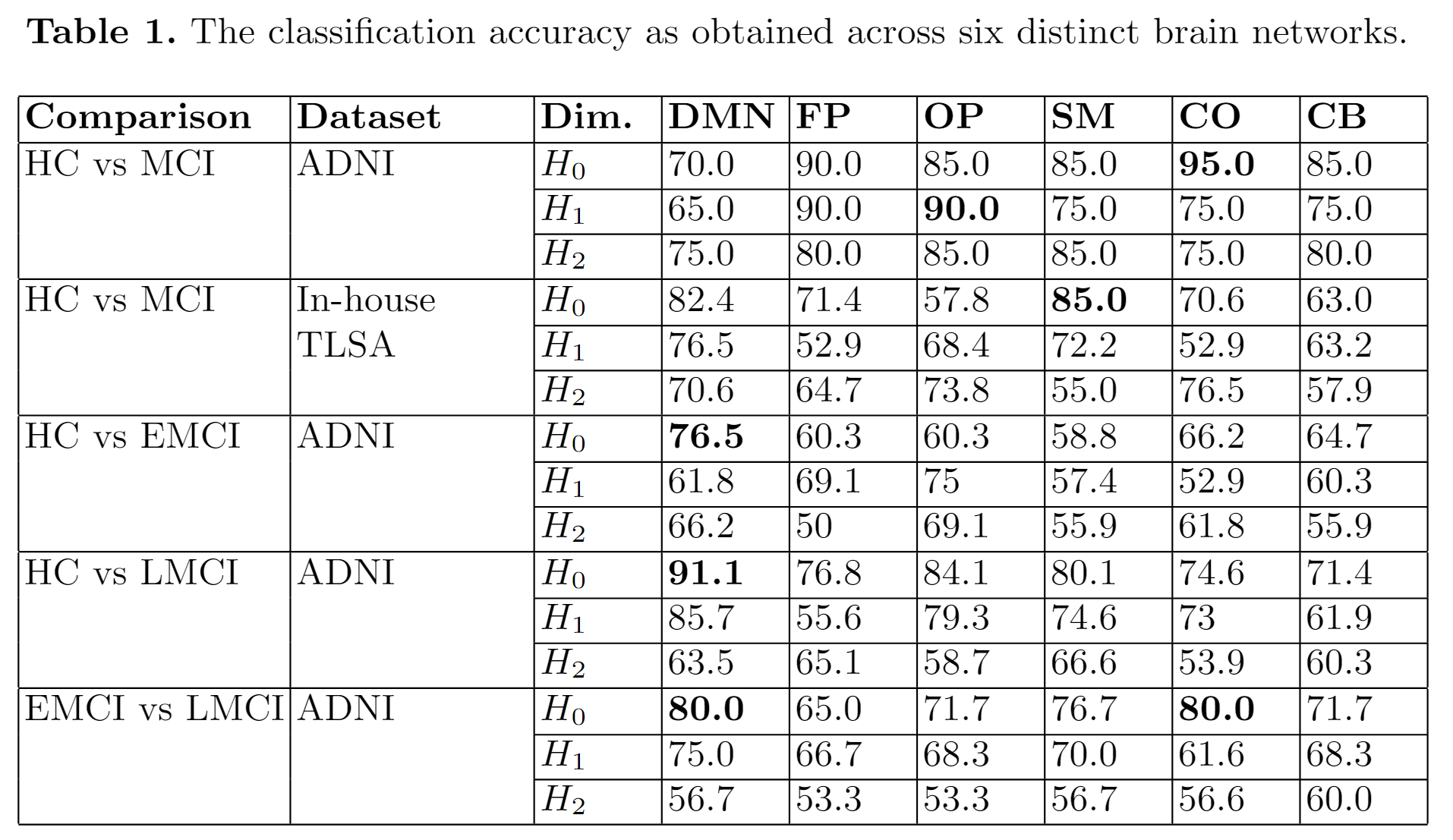
在六个不同的大脑网络中获得的分类准确性。
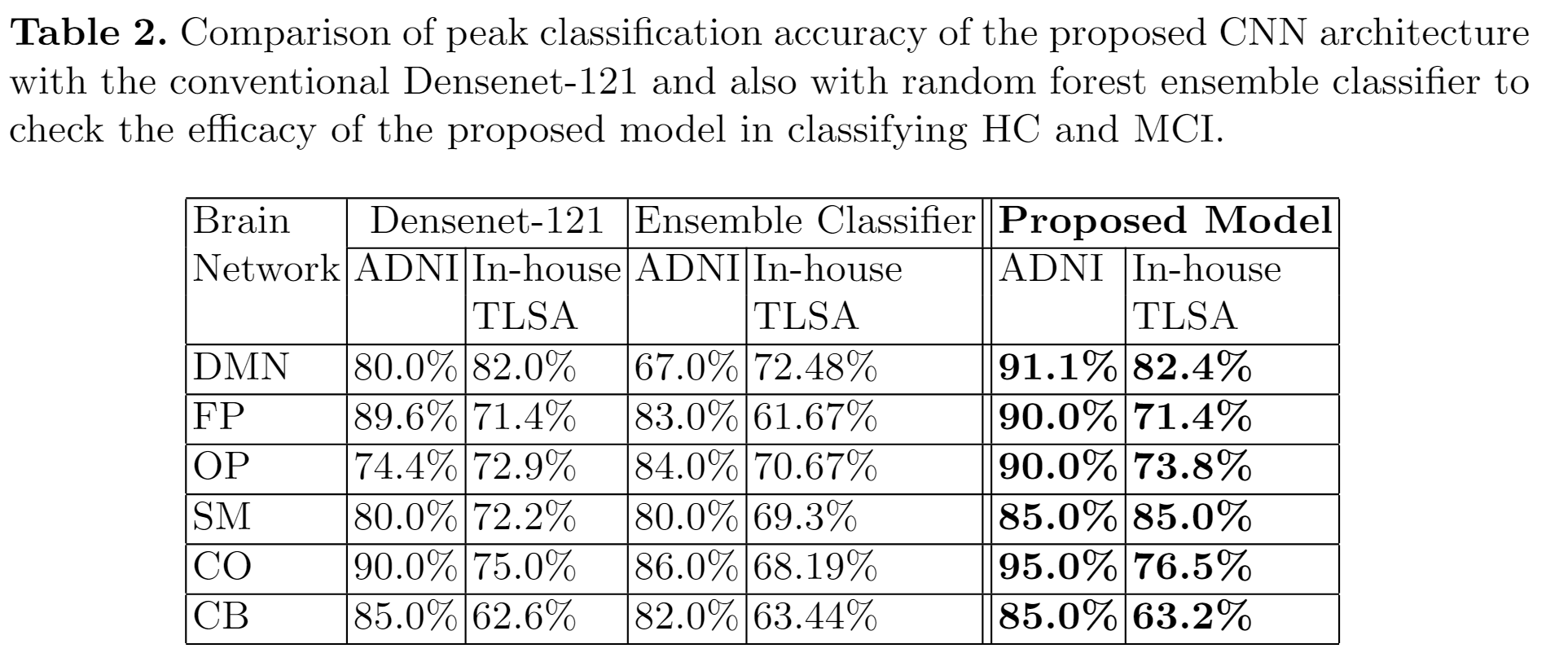
所提出的CNN架构的峰值分类精度与传统的Densenet-121以及随机森林集成分类器进行比较
与使用fMRI数据区分疾病亚型以及区分MCI及其亚型的最新最先进技术的比较分析。

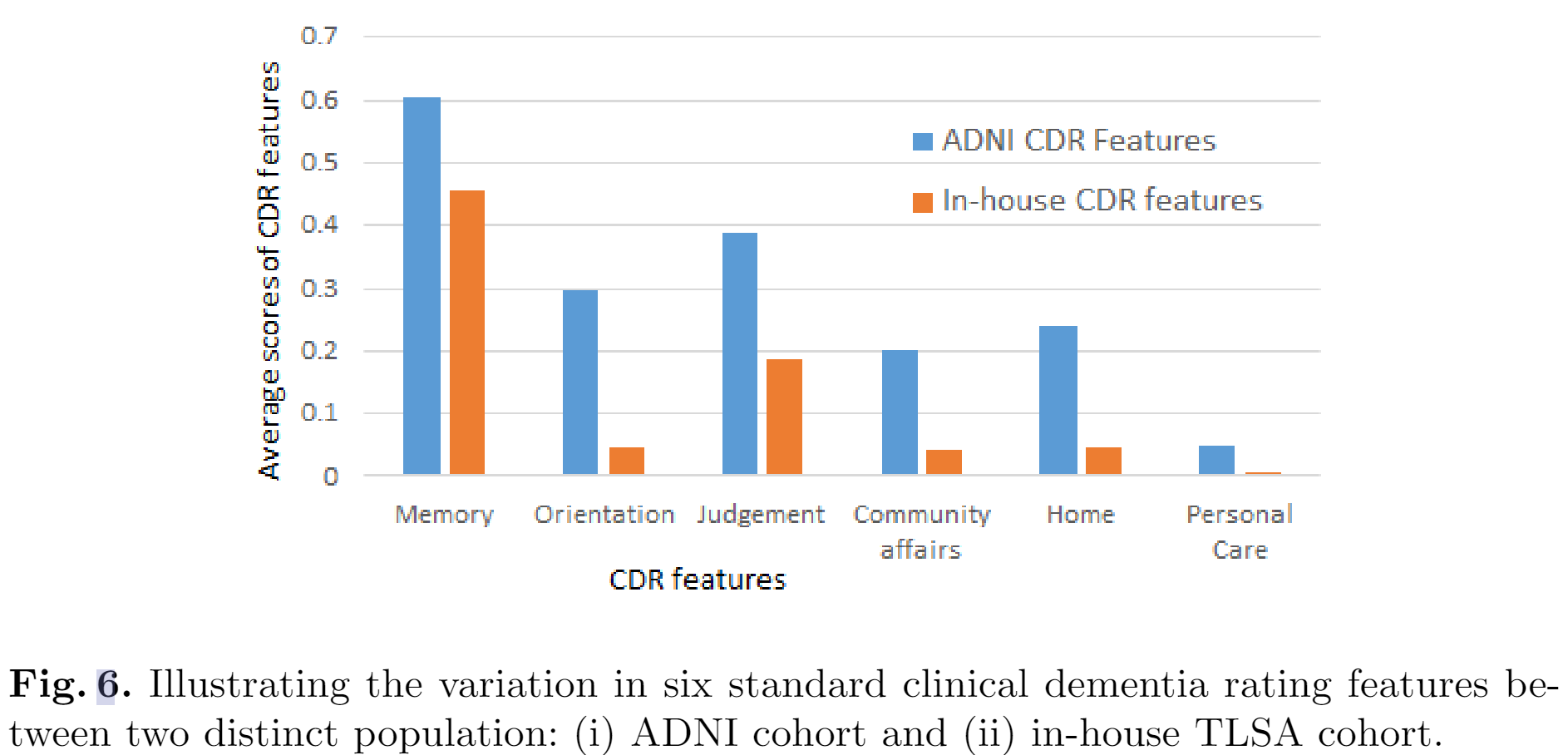
说明两个不同人群之间六个标准临床痴呆评分特征的差异:(i)ADNI队列和(ii)内部TLSA队列。