这是一篇来自大连理工的图像描述的工作，图像描述一般都是使用自回归模型，很少研究扩散模型，但是自回归模型会有错误累积的问题，本文针对多样性有限问题提出了一个轻量级的前缀扩散模型。文章的主要贡献在于通过将图像嵌入作为前缀，解决扩散模型的多模态问题。

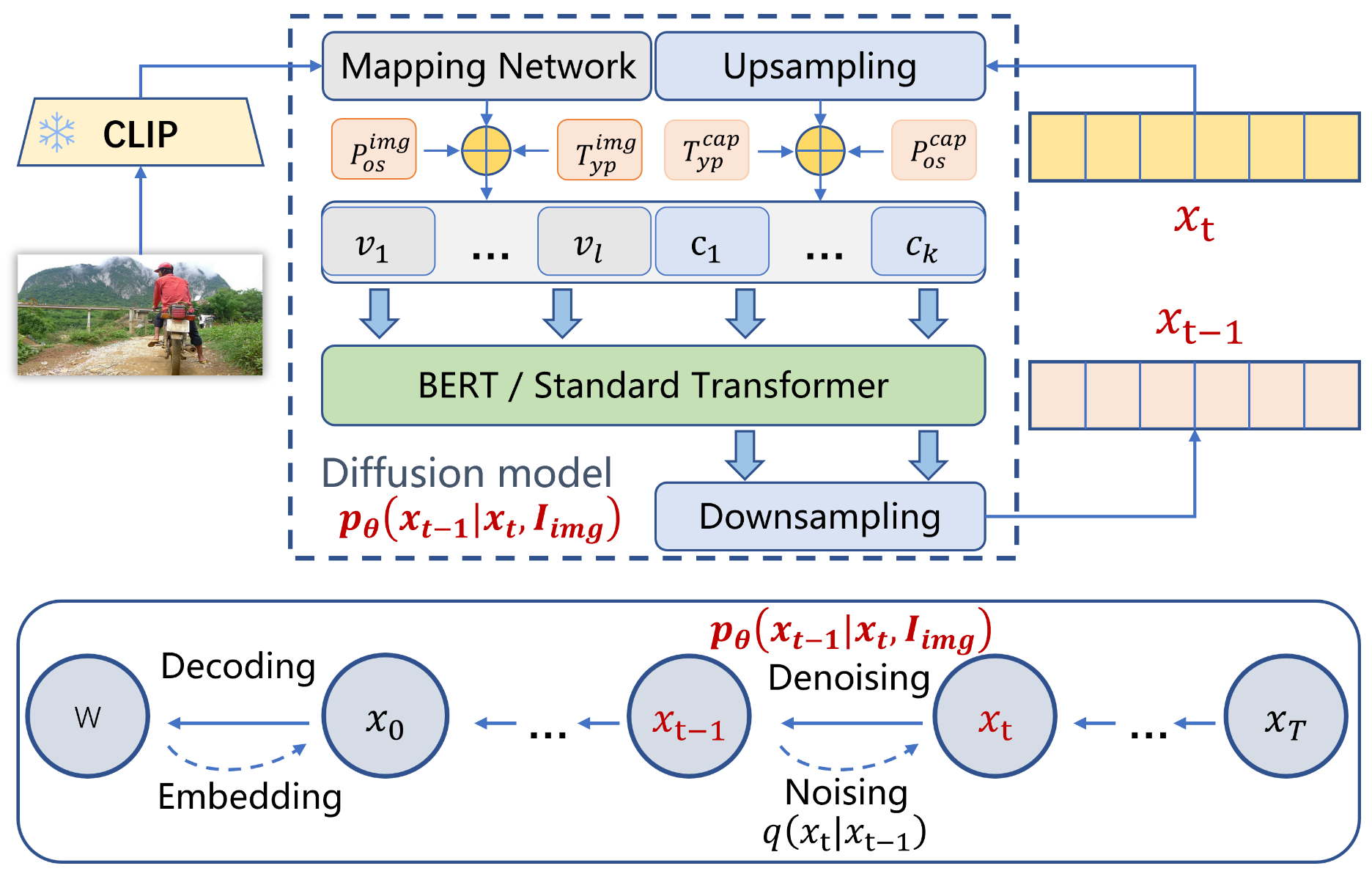
输入图片通过CLIP编码器抽取特征，然后输入它们到映射网络获得前缀图像嵌入。然后在扩散模型的去噪过程中，拼接前缀图像嵌入和标题嵌入。拼接的向量被输入到BERT/Transformer中。训练过程只有映射网络和BERT/Transformer的参数会被更新。

前向过程：与Diffsion-LM相同，使用一个嵌入函数EMB(.)将离散词语映射到一个连续空间。图片描述被定义为K个词，实验中发现嵌入维度设为48效果比较好。在前向过程中，扩散模型根据方差列表beta1,...,betaTbeta_1,...,beta_T逐步添加噪声训练样本。前向过程没有可学习的参数，xtx_t通过下列公式获得：

xt=1−βtxt−1+βtϵx_t=\sqrt{1-\beta_t}x_{t-1}+\sqrt{\beta_t}\epsilon

其中ϵ∼N(0,1)\epsilon\sim N(0,1)，βt:0.01→0.03\beta_t:0.01\rightarrow0.03表示扩散步骤中方差调度的超参数。论文尝试了不同的噪声方法，截断线性噪声调度（truncation linear noise schedule）方法效果最好。

反向过程：拟过程从xT∼N(0,I)x_T\sim N(0,I)中生成新样本，通过下列逆扩散过程采样数据：

pθ(xt−1∣xt,Iimg)=N(xt−1;μθ(xt,Iimg),θ(t)2I)p_\theta(x_{t-1}\mid x_t,I_{img})=\mathcal{N}(x_{t-1};\mu_\theta(x_t,I_{img}),\theta(t)^2I)

其中IimgI_{img}表示来自CLIP的视觉信息。在反向过程中，μθ\mu_\theta是神经网络学习到的，θ(t)2\theta(t)^2是固定的方差。

μθ(xt,Iimg)=αt(1−αˉt−1)1−αˉtxt+αˉt−1βt1−αˉtx0θ(t)2=1−αˉt−11−αˉtβt\mu_\theta(x_t,I_{img})=\frac{\sqrt{\alpha_t}(1-\bar{\alpha}_{t-1})}{1-\bar{\alpha}_{t}}x_t+\frac{\sqrt{\bar{\alpha}_{t-1}}\beta_t}{1-\bar{\alpha}_t}x_0 \\ \theta(t)^2=\frac{1-\bar{\alpha}_{t-1}}{1-\bar{\alpha}_{t}}\beta_t

通过下列公式获得x0x_0：

x0=1αˉt(xt−1−αˉz~)x_0=\frac{1}{\sqrt{\bar{\alpha}_t}}(x_t-\sqrt{1-\bar{\alpha}}\tilde{z})

通过深度神经网络（例如Transformer）获得z~\tilde{z}：

z~=Φ(xt,Iimg,t)\tilde{z}=\Phi(x_t,I_{img},t)

Φ\Phi就是模型中的虚线框，本文尝试了BERT和原始Transformer，与其它连续扩散方法不同的地方是，本文方法将图像特征注入的过程改变了caption空间中的原始均值，如图所示：

通过CILP+MLP获得ll长度的视觉前缀（图中的v1v_1到vlv_l），xtx_t通过上采样网络获得图中的c1c_1到ckc_k序列，然后分别加上位置嵌入和类型嵌入之后再拼接成一个序列一起输入给模型，后部分输入经过模型的输出通过下采样获得扩散模型的xt−1x_{t-1}。

解码过程：通过CLIP分数增强图像和描述文本的相似性，利用CLIP嵌入可以计算图像和nn个候选描述之间的余弦相似度,然后选择相关的文本描述。该模型可以生成具有不同高斯噪声的不同文本描述，所以可以通过这种方法进行检索。

实验：因为现在用不到这个模型和也不做图像描述任务，实验过程暂时不看，后续如果看了再更新。